Hierarchical Generalized Additive Models
Assigned Reading:
- Pedersen, E. J., Miller, D. L., Simpson, G. L., & Ross, N. (2019). Hierarchical generalized additive models in ecology: an introduction with mgcv. PeerJ, 7, e6876.
- Lawton, D., Scarth, P., Deveson, E., Piou, C., Spessa, A., Waters, C., & Cease, A. J. (2022). Seeing the locust in the swarm: accounting for spatiotemporal hierarchy improves ecological models of insect populations. Ecography, 2022(2).
Overview
Invasive plants cause immense ecological and economic damage. For example, in forested lands, invasive grasses can change fire regimes, invasive shrubs can reduce native tree regeneration, and invasive trees can reduce timber production. Determining patterns in 1) invasive plant abundance increases/decreases over time and 2) spatial distribution across forested lands could help managers assess potential risks to their lands. For today’s lab, we’re going to be using hierarchical generalized additive models (HGAMs) to help us make these determinations–and add some theoretical flavor to them.
For the abundance increase/decrease over time issue, we will ask:
- Does functional group (e.g., growth habits such as graminoid, tree, shrub, etc.) or taxonomy (e.g., order) best explain invasive plant abundance changes?
For the spatial distribution issue, we will ask:
- How do abundance patterns differ by growth habit across space?
The first question will help us understand how to construct HGAMs from our hypotheses, appraise HGAM fits, and conduct model selection with HGAMs. Through the second question, we will learn to do spatial predictions (i.e., making predictive maps) with our model outputs.

Data description
The data you will be using is from the U.S. Forest Service’s “Forest Inventory and Analysis” (FIA) dataset. The FIA dataset is taken on public and private forested and timber lands throughout the U.S. on specific plots. The plots are revisited approximately every 4 - 5 years, but some plots are never revisited. One of the data collected at each plot is percent cover of various invasive plants. Here, I used the “rFIA” R package to extract invasive species cover data from the Eastern U.S. from 2001 - 2020. I also extracted growth habits and orders of each plant species from the USDA Plants Database. Below is a table with descriptions of columns in each dataset:
| Data File Name | Column Name | Description |
|---|---|---|
| FIA_Invasives_GrowthTaxonomy.csv | SCIENTIFIC_NAME | Genus and species |
| GrowthHabit1 | Primary growth habit | |
| GrowthHabit2 | Secondary growth habit, if applicable | |
| GrowthHabit3 | Tertiary growth habit, if applicable | |
| GrowthHabit_Number | Number of growth habits | |
| Order | Order of the species | |
| COMMON_NAME | Species’ common name | |
| FIA_Invasives_Cover.csv | Year | years 2001 - 2020 |
| pltID | Unique identifier for each FIA plot | |
| SCIENTIFIC_NAME | Genus and species | |
| COMMON_NAME | Species’ common name | |
| cover | areal cover of invasive species (acres) | |
| Longitude | decimal degrees longitude | |
| Latitude | decimal degrees latitude |
Let’s load the data and join the two files:
# List of packages necessary to run this script:
require(librarian, quietly = TRUE)
shelf(tidyverse,
mgcv, # For checking model convergence
MuMIn, # for model selection
gratia, # for ggplot functionality with mgcv
modelr, # for cross-validation
vroom, # for loading data FAST
sf, # making spatial objects and maps
lib = tempdir(),
quiet = TRUE)
# Set random number
set.seed(9903)
# Set the web address where R will look for files from this repository
# Do not change this address
repo_url <- "https://raw.githubusercontent.com/LivingLandscapes/Course_EcologicalModeling/master/"
# Load invasive species cover data
fia <- read_csv(paste0(repo_url, "data/FIA_Invasives_Cover.csv"))
# Load invasive species metadata
spp_info <- read_csv(paste0(repo_url, "data/FIA_Invasives_GrowthTaxonomy.csv"))
# Join the cover and metadata
fia <- left_join(fia, spp_info)
# Some preparations for mgcv
fia <-
fia %>%
mutate(across(c(Order, GrowthHabit1, GrowthHabit2, GrowthHabit3, SCIENTIFIC_NAME, pltID),
as.factor), # mgcv wants factors for random effects
cover_0.001 = cover + 0.001, # for log link
across(c(Year, Latitude, Longitude),
~ (.x - mean(.x)) / sd(.x),
.names = "{.col}_scaled")) # scale covariatesData Exploration
On your own, familiarize yourself with the data. Below, you can see that we’re dealing with >100k rows and a few potential grouping variables.
## [1] 101979 16# How many unique values in each column?
fia %>%
summarize(across(everything(), ~ length(unique(.x))))## # A tibble: 1 × 16
## Year pltID SCIENTIFIC_NAME COMMON_NAME cover Longitude Latitude GrowthHabit1
## <int> <int> <int> <int> <int> <int> <int> <int>
## 1 21 29994 74 74 16069 29955 29916 6
## # ℹ 8 more variables: GrowthHabit2 <int>, GrowthHabit3 <int>,
## # GrowthHabit_Number <int>, Order <int>, cover_0.001 <int>,
## # Year_scaled <int>, Latitude_scaled <int>, Longitude_scaled <int># What's the max, min, mean, and median of the "cover" column?
fia %>%
summarize(Mean = mean(cover),
Median = median(cover),
Min = min(cover),
Max = max(cover))## # A tibble: 1 × 4
## Mean Median Min Max
## <dbl> <dbl> <dbl> <dbl>
## 1 0.118 0.05 0 1## [1] 1## **QUESTION**: Given there is only a single zero in the cover data, how does that affect the scope of our inference?
# Let's make a map! First, convert to an sf object for mapping
fia_sf <- st_as_sf(fia,
crs = st_crs(4326),
coords = c("Longitude", "Latitude"))
# Get a US states map
states <- map_data("state") # Map of US states
# # Make a map to show where the weather stations are:
# ggplot() +
# geom_polygon(data = states %>%
# filter(region %in% c("kentucky","tennessee", "mississippi", "texas",
# "alabama", "georgia", "florida", "oklahoma",
# "arkansas", "south carolina", "virginia",
# "louisiana", "north carolina", "maryland")
# ),
# mapping = aes(x = long, y = lat, group = group),
# fill = "white",
# color = "black") +
# geom_sf(data = fia_sf,
# shape = 15,
# alpha = 0.5,
# mapping = aes(color = Year)) +
# theme_bw() +
# theme(panel.grid.minor = element_blank(),
# axis.text.x = element_text(angle = 330),
# axis.text = element_text(size = 6,
# hjust = 0.1)) +
# xlab("Longitude") +
# ylab("Latitude")Sidenote: Should you ‘gam’ or ‘bam’?
This is a logistic issue relevant to using (H)GAMs with large datasets. The ‘gam’ function is the main mgcv way to run a (hierarchical) generalized additive model, but if you’re analyzing a lot of data (e.g., >100k rows), you may consider switching to the ‘bam’ function. The outputs are very similar, but there are some differences due to some shortcuts the ‘bam’ function uses behind the curtains. If you’re interested, read about that here and also here.
Also, to prove the difference in runtimes, check this out:
# # runtime for 'bam'
# system.time(
# bam(cover_0.001 ~
# te(Longitude_scaled, Latitude_scaled) +
# s(Year_scaled) +
# s(Year_scaled, GrowthHabit1, bs = "fs"),
# family = Gamma("log"),
# data = fia,
# discrete = TRUE,
# method = "fREML")
# )
#
# # runtime for 'gam'
# system.time(
# gam(cover_0.001 ~
# te(Longitude_scaled, Latitude_scaled) +
# s(Year_scaled) +
# s(Year_scaled, GrowthHabit1, bs = "fs"),
# family = Gamma("log"),
# data = fia,
# method = "REML")
# )Abundance changes: Growth habit or taxonomy?
“Random Slope”: Model GS
Let’s try our first HGAM: estimate a global function for our main covariate of interest (Year) plus a individual-level random slope for Year per growth habitat/order. We’ll also throw latitude and longitude into a tensor smooth to account for spatial autocorrelation.
On your own, investigate each model diagnostic call (commented out in the chunk below) and interpret. Look at the R help for more information, and ask Caleb if you have more questions.
# Create model GS using bam()
growth_modGS <-
bam(cover_0.001 ~
te(Longitude_scaled, Latitude_scaled) + # tensor smooth lets latitude/longitude 'interact'
s(Year_scaled) +
s(Year_scaled, GrowthHabit1, bs = "fs"),
family = Gamma("log"), # Why this link?!
data = fia,
discrete = TRUE,
method = "fREML") # need to use fREML for fast fitting.
# # Some basic model diagnostics
# summary(growth_modGS)
# gam.check(growth_modGS)
# gratia::appraise(growth_modGS)
order_modGS <-
bam(cover_0.001 ~
te(Longitude_scaled, Latitude_scaled) + # tensor smooth lets latitude/longitude 'interact'
s(Year_scaled) +
s(Year_scaled, Order, bs = "fs"),
family = Gamma("log"), # Why this link?!
data = fia,
discrete = TRUE,
method = "fREML") # need to use fREML for fast fitting.
# # Some basic model diagnostics
# summary(order_modGS)
# gam.check(order_modGS)
# gratia::appraise(order_modGS)Okay, so the models aren’t the greatest for a few reasons. On your own, check out the gratia::appraise calls that are commented out, and list some issues with these models.
“Group smoothers with differing wiggliness (no global smoother)”: Model I
Okay, now let’s create models for our other hypothesis (order or growth habit alone best explain changes in invasive species abundance, and abundance changes occur idiosyncratically based on growth habit/order). To do this, we’ll use model “I” per Pederson et al. (2019).
# Growth habit
growth_modI <-
bam(cover_0.001 ~
te(Longitude_scaled, Latitude_scaled) +
s(Year_scaled, by = GrowthHabit1) +
s(Year_scaled, bs = "re"), # Why include this??
family = Gamma("log"),
data = fia,
discrete = TRUE,
method = "fREML")
# Order
order_modI <-
bam(cover_0.001 ~
te(Longitude_scaled, Latitude_scaled) +
s(Year_scaled, by = Order) +
s(Year_scaled, bs = "re"),
family = Gamma("log"),
data = fia,
discrete = TRUE,
method = "fREML")On your own, run the model diagnostics and compare to diagnostics from Model I. Are there improvements, and if so, where do you see them? Should we consider increasing “k” for any of the smoothers?
Model selection
We learned from the Pedersen et al. (2019) paper that we can use AIC to compare HGAMs, which is awesome! But–model selection via AIC should not be our stopping point. In this section, we’re going to dip our toes into cross validation to compare the predictive power of HGAMs.
But first, let’s just see what AIC(c) has to say about our two HGAMs:
model.sel(list(growth_modGS = growth_modGS,
order_modGS = order_modGS,
growth_modI = growth_modI,
order_modI = order_modI))## Model selection table
## (Int) s(Yer_scl) s(Yer_scl,GH1,"fs") te(Lng_scl,Ltt_scl)
## order_modGS -2.116 + +
## growth_modGS -1.873 + + +
## order_modI -1.679 +
## growth_modI -1.644 +
## s(Yer_scl,Ord,"fs") s(Yer_scl,"re") s(Yer_scl,GH1) s(Yer_scl,Ord)
## order_modGS +
## growth_modGS
## order_modI + +
## growth_modI + +
## df logLik AICc delta weight
## order_modGS 98 125833.3 -251468.9 0.00 1
## growth_modGS 61 125463.2 -250803.0 665.93 0
## order_modI 130 125517.7 -250773.6 695.33 0
## growth_modI 76 124972.1 -249790.8 1678.15 0
## Models ranked by AICc(x)We have a very clear winner per AICc rankings: the order random slope (GS) model. In your own words, articulate what that means ecologically.
Cross validation
Model selection is not the only way to check for model performance. Here, we’ll do a “quick and dirty” cross validation exercise to see how our models perform relative to the observations–and in comparison with each other. For brevity’s sake, we’ll just look at the top two models from our model selection.
# Create training and testing data.frames
train_df <-
sample_n(fia %>% mutate(id = 1:n()),
ceiling(nrow(fia)/10)) # Using 90% of the data for training
test_df <-
anti_join(fia %>% mutate(id = 1:n()),
train_df, by = "id") # Use the remaining 10% of the data to test
# train models
order_modGS_train <-
bam(cover_0.001 ~
te(Longitude_scaled, Latitude_scaled) +
s(Year_scaled) +
s(Year_scaled, Order, bs = "fs"),
family = Gamma("log"),
data = fia,
discrete = TRUE,
method = "fREML")
growth_modGS_train <-
bam(cover_0.001 ~
te(Longitude_scaled, Latitude_scaled) +
s(Year_scaled) +
s(Year_scaled, GrowthHabit1, bs = "fs"),
family = Gamma("log"),
data = fia,
discrete = TRUE,
method = "fREML")
# Root mean square error and mean absolute error to test models
data.frame(Model = c("order_modGS", "growth_modGS"),
RMSE = c(rmse(order_modGS_train, test_df),
rmse(growth_modGS_train, test_df)),
MAE = c(mae(order_modGS_train, test_df),
mae(growth_modGS_train, test_df)))## Model RMSE MAE
## 1 order_modGS 2.451044 2.394720
## 2 growth_modGS 2.443929 2.390163Oof! Looks like both our quick and dirty cross-validation tests show the models have negligible differences in predictive ability. Also, the values of MAE and RMSE suggest that our models are pretty crumby at predictions!! Just goes to show that we need to assess models from multiple angles. On your own, consider what would make these models better predictors.
Visualize HGAM smooth estimates
Now, let’s plot the smooth estimates from our top model. Recall what a “smooth estimate” is in a generalized additive model. How does it differ from a “prediction?”
There are multiple ways to visualize the smooth estimates, but here, we’ll take the easy way out and use functions from the “gratia” package.
# Luckily, the gratia package has some nice functions for creating customized model prediction plots:
# See the exact names of the smooths in the model object
smooths(order_modGS)## [1] "te(Longitude_scaled,Latitude_scaled)"
## [2] "s(Year_scaled)"
## [3] "s(Year_scaled,Order)"# Save smooth estimates.
sm <- smooth_estimates(order_modGS)
# Plot the global "s(Year_scaled)" estimate
sm %>%
filter(.smooth == "s(Year_scaled)") |>
add_confint(coverage = 0.80) |> # 80% confidence intervals
ggplot(aes(y = .estimate,
x = Year_scaled)) +
geom_ribbon(aes(ymin = .lower_ci,
ymax = .upper_ci),
alpha = 0.3,
fill = "gray70") +
geom_line(linewidth = 1) +
geom_hline(data = data.frame(yintercept = 0),
mapping = aes(yintercept = yintercept),
linetype = 2,
color = "darkred") + # Adding to make it clear where confidence intervals encompass zero.
theme_bw() +
ylab("Estimate")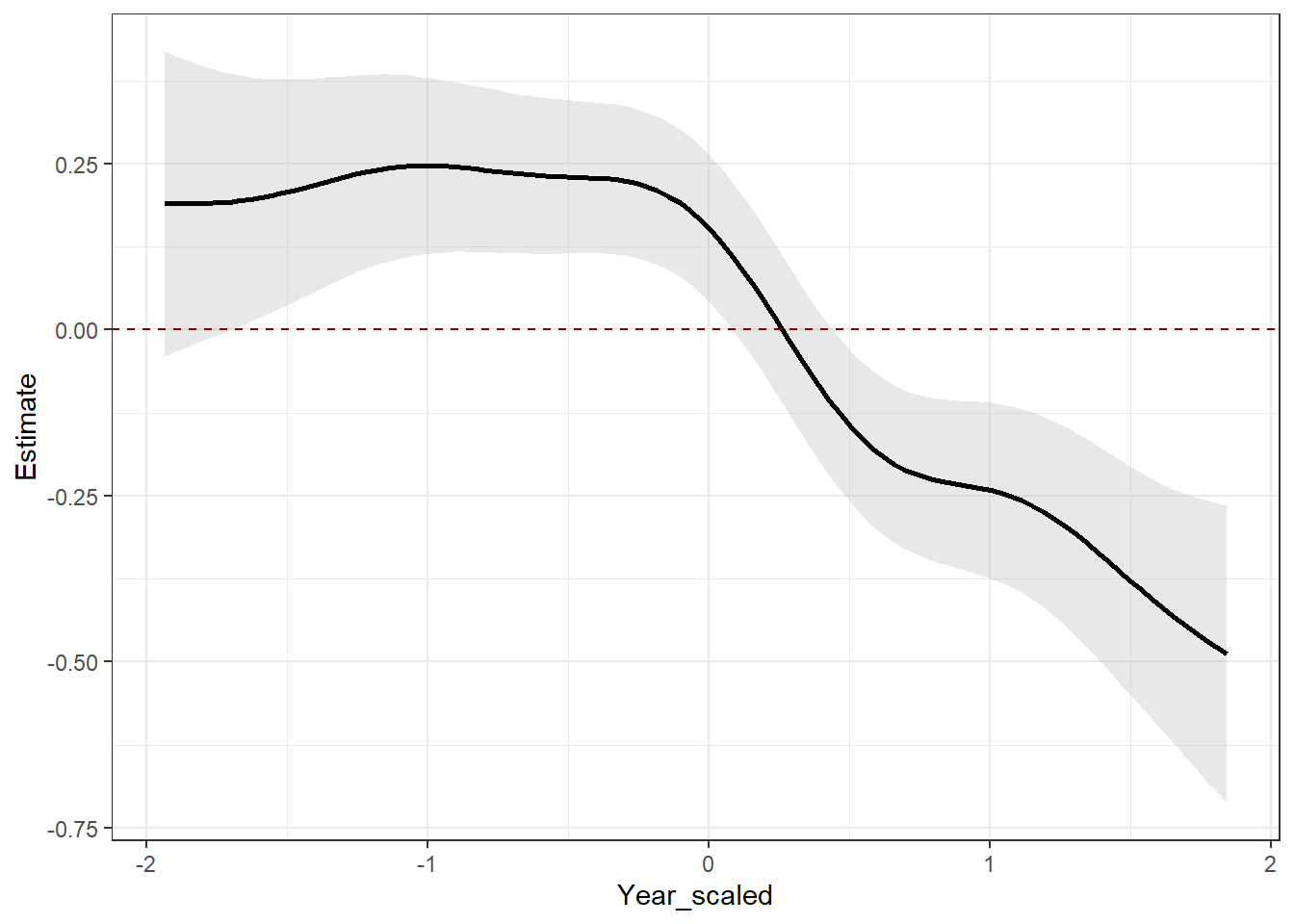
# Plot the factor smooths for each growth habit
sm %>%
filter(.smooth == "s(Year_scaled,Order)") |>
add_confint(coverage = 0.80) |> # 80% confidence intervals
ggplot(aes(y = .estimate,
x = Year_scaled,
group = Order)) +
geom_ribbon(aes(ymin = .lower_ci,
ymax = .upper_ci),
alpha = 0.3,
fill = "gray70") +
scale_color_viridis_d() +
geom_line(linewidth = 1,
mapping = aes(color = Order)) +
geom_hline(data = data.frame(yintercept = 0),
mapping = aes(yintercept = yintercept),
linetype = 2,
color = "darkred") + # Adding to make it clear where confidence intervals encompass zero.
theme_bw() +
# facet_wrap(~ Order) +
ylab("Estimate")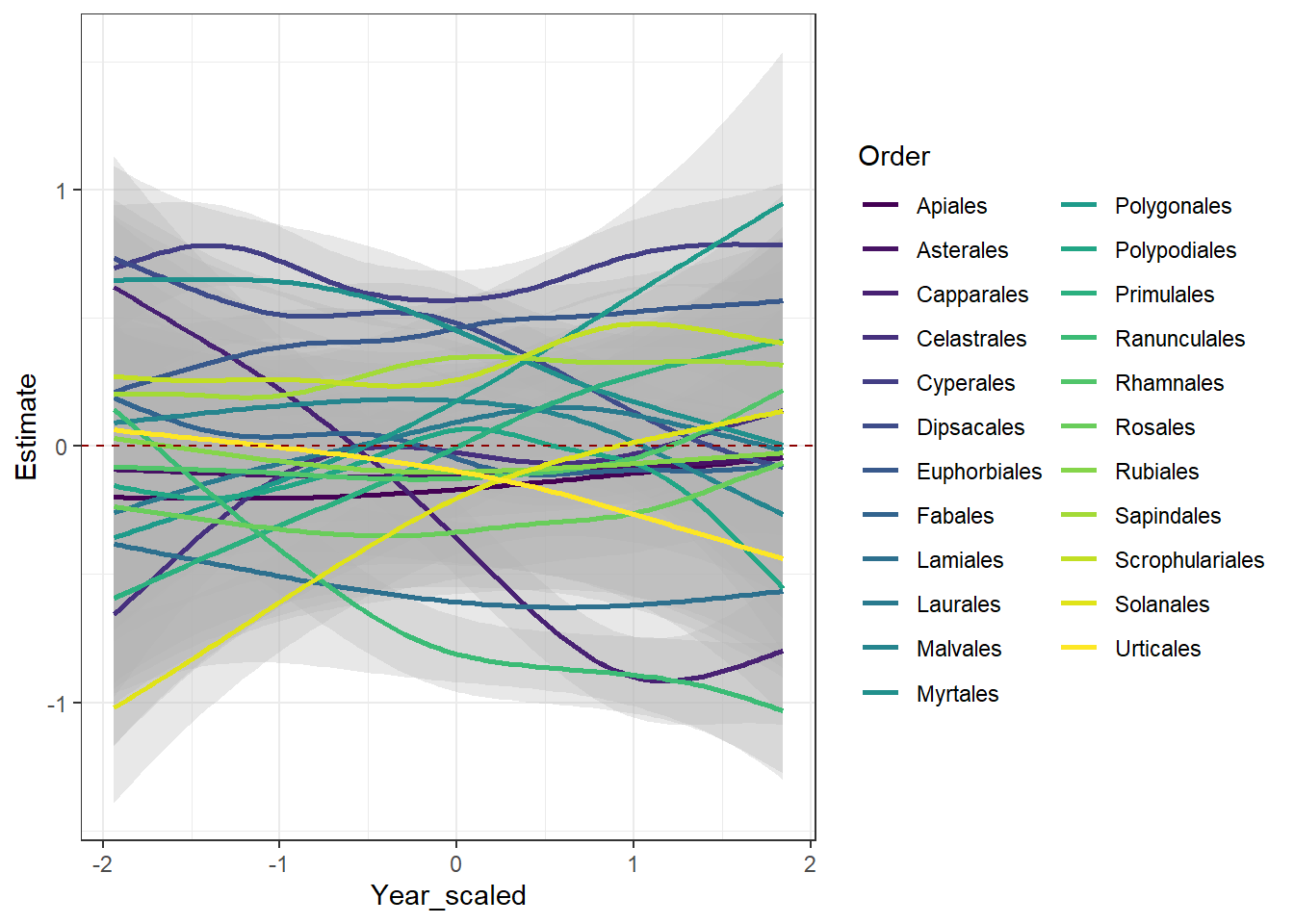
On your own, interpret the prediction plots. How does the global smoother ( “s(Year_scaled)” ) estimate compare to the individual factor smooths ( “s(Year_scaled,Order)” )? What does it mean for the estimate to be above the zero line, encompassing the zero line, and below the zero line?
IMPORTANT: Circle back to a question from the beginning of the lab. Given the trend you’re seeing in the “s(Year_scaled)” plot, what does it mean for our inferece that there are no zeroes in this dataset???
Spatial predictions
In this final section, we’re going to deviate from our hypotheses a bit in order to show you how to do some spatial predictions–and then create maps with your spatial predictions. There are MANY resources that show how to do this–particularly for raster data. So to be additive and not repetitive, here, we will predict an HGAM’s outputs across a vector dataset.
To be even more fun, we’ll make a “honeycomb” (hexagonal) map. There are some actual reasons to use a honeycomb instead of a “fishnet” (square grid), some of which are listed in this paper. Also, the nature of the FIA data lends itself to being re-aggregated into large polygons.
As a first step, let’s make the honeycomb!
# First, convert the FIA data to an sf object
fia_sf <- st_as_sf(fia,
crs = st_crs(4326), # This number is the code for the Lat/Long Coordinate Reference System. You can look other codes up (e.g., UTM zone 14 = 32614)
coords = c("Longitude", "Latitude"))
# Read in a shapefile with all extensions of the US states of interest
states <-
st_read(paste0("/vsicurl/", # need to add this to get all shapefile extensions
repo_url,
"data/US_States/cb_2018_us_state_5m.shp")) %>%
filter(NAME %in% c("Kentucky","Tennessee", "Mississippi",
"Alabama", "Georgia", "Florida",
"Arkansas", "South Carolina", "Virginia",
"Louisiana", "North Carolina"))## Reading layer `cb_2018_us_state_5m' from data source
## `/vsicurl/https://raw.githubusercontent.com/LivingLandscapes/Course_EcologicalModeling/master/data/US_States/cb_2018_us_state_5m.shp'
## using driver `ESRI Shapefile'
## Simple feature collection with 56 features and 9 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -179.1473 ymin: -14.55255 xmax: 179.7785 ymax: 71.35256
## Geodetic CRS: NAD83# Create hexagonal grid...
honeycomb_grid <-
st_make_grid(st_union(states), # Need to combine all state polygons
cellsize = 0.5,
what = "polygons",
square = FALSE) %>%
st_sf() %>% # Force geometry into a sf "data.frame" like object
rowid_to_column('hex_id') %>% # Make an ID column for the hex polygons
st_make_valid() # Not sure why we need this, but it was necessary for the intersection to work haha
# ... and clip to our study extent (states)
honeycomb_grid <-
st_intersection(honeycomb_grid,
st_union(states))Now that we’ve made the honeycomb polygons, let’s make the data to predict onto. To do that, we’ll need coordinates (latitude and longitude, scaled). But… which coordinates do we choose? For raster cells, it’s pretty easy as every pixel has an associated coordinate. But for vector data, there are an infinite number of coordinates we could choose from.
On your own, think of a solution to this problem! Once you’ve got an idea, reveal the code below.
# (One) solution: get hexagonal centroids!
honeycomb_centroids <- st_centroid(honeycomb_grid)
# Scale prediction covariates--on the same scale as the covariates used for fitting the model!
nd_0 <- data.frame(Latitude_scaled = rep((st_coordinates(honeycomb_centroids)[,2] - mean(fia$Latitude)) / sd(fia$Latitude), 2),
Longitude_scaled = rep((st_coordinates(honeycomb_centroids)[,1] - mean(fia$Longitude)) / sd(fia$Longitude), 2),
Year_scaled = rep(c(min(fia$Year_scaled),
max(fia$Year_scaled)),
each = nrow(honeycomb_centroids)), # Since we're not interested in time, pick most recent year.
hex_id = rep(honeycomb_centroids$hex_id, 2))
# Make a data.frame for prediction
nd <-
do.call(rbind,
lapply(unique(fia$Order),
function(X) {
# We need to get latitudes and longitudes for each grid cell
# for each growth habit. We'll use a lapply function to do this
# quickly.
df <- data.frame(Order = X,
nd_0)
return(df)
}))Final step: make the prediction and the map! You should be familiar with all this from previous labs. The only new parts are the color ramp and the “geom_sf” code. Thankfully, the folks who created the “sf” package made it compatable with ggplot, so all you need is an sf object (e.g., our “fia_sf” object). The rest takes care of itself!
# Prediction. We won't worry about the standard error/confidence here. However, it's best practice to create maps of uncertainty whenever you create a predictive map.
spFit_pred <-
predict(order_modGS,
newdata = nd,
type = "response")
# Create prediction data.frame
spFit_pred_df <- data.frame(fit = spFit_pred, nd)
# Join prediction with the honeycomb grid
pred_sf <-
left_join(honeycomb_grid,
spFit_pred_df)
# Create a custom color ramp. We'll need this because the predictions are CRAZY skewed. So if we allowed R to generate a color ramp for us, we wouldn't be able to see the nuance in the predictions.
colorBreaks <- seq(min(pred_sf$fit),
max(pred_sf$fit),
0.01)
colorRamp <- c(colorRampPalette(rev(c("#fde725", # these are viridis color-blind friendly colors
"#5ec962",
"#21918c",
"#3b528b",
"#440154")),
bias = 1.5)(length(colorBreaks[colorBreaks < quantile(pred_sf$fit, 0.99)])), # Cutoff at 99th quantile
rep("#fde725", length(colorBreaks) - length(colorBreaks[colorBreaks < quantile(pred_sf$fit, 0.99)])))
# Make the map! Let's just use the first year (2001)
ggplot(pred_sf %>% filter(Year_scaled == min(Year_scaled)),
aes(fill = fit)) +
facet_wrap(~ Order, ncol = 6) +
scale_fill_gradientn(colors = colorRamp,
name = "Cover") +
geom_sf()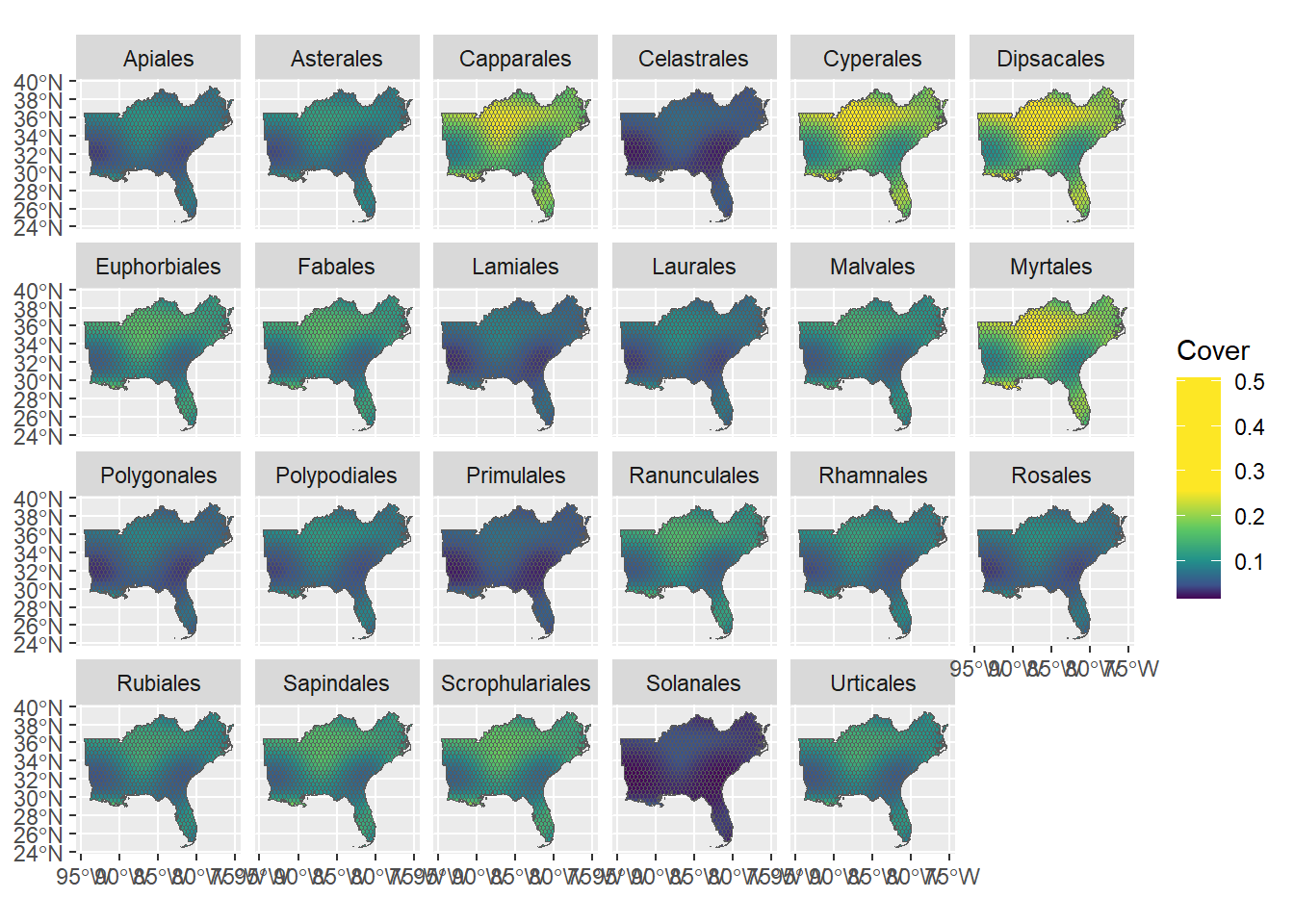
We did it!
Discussion questions
Given the global time smooth estimate ( “s(Year_scaled)” ), what would the prediction maps look like in the final year of our FIA data?
What are similarities and differences in the prediction maps? What aspects of the HGAM we used makes them similar/different?
What kind(s) of HGAM would create very different predictive maps/smooth estimates for the different order?
Given there were no zeroes in our response variable (cover), what can these models actually tell us? What can they not tell us? What would be a way to add zeroes to the data?